先週の木曜日から仕事が立て込んでいて、学校HPの更新をすることができませんでした。今日から更新を再開しますので、よろしくお願いいたします。
11月13日(月)の2校時に、5年2組の教室で算数の校長参観授業をしました。「面積の求め方を考えよう」で、本時の目標は「台形の面積も求め方を既習の図形に帰着していろいろな方法で考え、説明することができる」です。

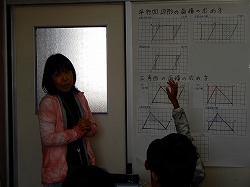



学習コーナーが作ってあり、そこには三角形や平行四辺形の面積の求め方の様々なパターンがまとめてあり、既習事項が確認できるようになっていました。先生は、三角形や平行四辺形の面積の求め方について発問し、子ども達に答えさせながら確認していました。じつは、これが台形の面積の求め方を考える「見通し」となり、手がかりになります。
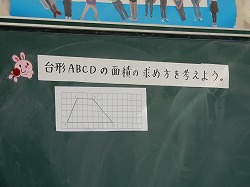









次に、黒板に台形の図形の描かれた大型の方眼紙を貼り、本時の課題の「台形ABCDの面積の求め方を考えよう」も貼り、本時の課題を把握しました。その後、この問題を解決する「見通し」、つまり大まかな解決法を発表させました。出てきたのは次の4つです。
・分けて移動する⇒分割・合体作戦
・2倍作戦
・ある形に変える
・たし引き作戦
このように〇〇作戦と名前をつけることで子ども達はイメージしやすくなり、問題解決のツールとして活用することがしやすくなります!





























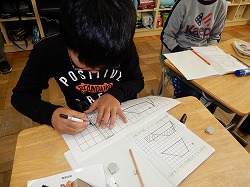







子ども達は本時の課題解決のための台形の描かれた方眼紙を2枚もらい(もちろんその方眼紙は、必要に応じて何枚ももらえるようになっていました)、そこに補助線を書いたり、自分なりの求積の方法を書き込んだり、切り抜いて組み合わせたりして、台形の面積を求める方法を表していました。さらに、それをノートに貼りました。担任の望月先生は机間巡視をしながら、必要に応じて個別指導をしながら、手元の座席表にそれぞれの子ども達の解決法を書き込んでいました。すべての考えが全体に発表できるような意図的指名をするために、台形の描かれた大型の方眼紙を特徴的な考え方をしている子に配りました。大型方眼紙を配ってもらった子ども達は、式や説明などの書き込みはせず、補助線や図形の組み合わせなどのみを示しました。これが、この後の全体の学び合いの「つなぎ」に役立ちます。自力解決の時間も「5分間でやりましょう」とか「あと2分間だけ延長します」と時間設定をしっかりして、授業全体を見据えながら指導している点も感心しました!

























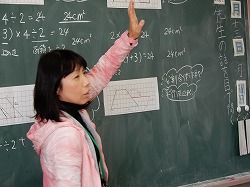






全体の学び合いの様子です。例えば、ある男の子が台形を2枚上下を逆さにしながらつなげて平行四辺形を作った大型方眼紙を貼り、「2倍作戦で平行四辺形を作りました」と発表した後、望月先生は「この式を教えてください」と発問し、違う子に式(12×4÷2=24 答え24㎠)を発表してもらいました。さらに「この12は何を表しているのですか?」と聞いて「上底+下底」であることを確認した後、「この4は何ですか」と質問し、「それは高さです」という答を得ました。「この÷2って何?」と聞き、台形を2倍したから割っていることを確認しました。このように、一人が発表して終わりではなく、一人の発表を多くの子ども達が解釈したり解説したりしながら、「つなぎ」ながら全員で理解しました。このような「つなぐ」学習を4種類の求積法で行いました。私がとても感心したのは、こうした「つなぐ」学習をしているとき、全員がそのやりとりをよく聞いていたことです! みんなで一人の考えを協力して解き明かしていくことは、子ども達にとってとても興味深いことなのですね! その証拠に、4種類の求積法の学習が終わった後、子ども達は「まだある! 先生、言いたい!!」と言っていましたが、発表したいというこれが大切なのです!!





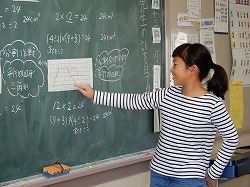

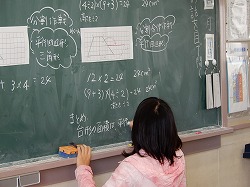
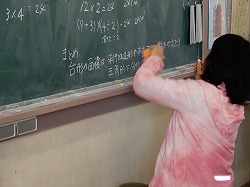





いよいよ本時の学習の核心に迫る学習にさしかかりました。「いろいろな考え方を出してもらったのだけど、考え方で似ているところはある?」と先生が本時のまとめにつながる発問をしました。「底の辺と上の辺をたしている」など出されましたが、先生が「台形の面積を求めるのに、台形をどのような形にしていますか?」と質問すると、子どもから「平行四辺形」「長方形」「三角形」が出されました。先生は子ども達の言葉を使い、黒板に「台形の面積は、平行四辺形や長方形に形をかえたり、三角形に分けたりすれば求めることができる」とまとめました。子どもと一緒に本時のまとめをしていく姿勢が素晴らしいです!!








最後に学習感想を書いて終わりました。ある女の子は「私は〇〇ちゃんの意見にとても驚きました。平行四辺形と三角形という2つを使って求めるという意見は全然考えませんでした」と書きましたが、友達の学習の様子とそれを自分がどう感じたのかが書かれてあり、学習感想としても、レベルの高いものになっていました!
素晴らしい学び合いの授業をした望月先生と、その指導に応えて高度な学習を展開した子ども達に大きな拍手を送ります!!
